发散性思维-点点思考-“1”的变换理解、达林顿管、MOS管立体结构、数电设计思考
最近事情实在多,今天球赛拼得两腿都伤,偶得空闲,正好整理下最近的一些东西、思考主要的内容还是多元化的,首先是数物给的思考题做“1”的傅里叶变换,经过长达两小时的思考终于自我理解了傅里叶的意义,真不愧是“第一”算法、然后讲讲平常有接触但是不怎么熟悉的达林顿管结构、MOS管的立体结构(不囿于书本上的平面结构)、最后就讲讲一个电路设计思路……
“1”的傅里叶变换与深度理解
傅里叶变换其实网上很多人有写相关的研究、理解的博客,感觉比较乱杂,所以还是得自己理解下。本质上其确实可以概括为就是函数从时域映射到频域(t——>f)但是这样还是比较抽象,毕竟信号处理还没学,所以下面就讲讲具体“1”的傅里叶变换
因为我已经理解到后面的结果处,我觉得如果没有提前学过冲激函数,然后突然用到冲激函数就显得很突兀,所以我试着倒着讲 - - “1”因为是一个常函数,也就是说可以理解为在频域下我无论取什么频率,其信号幅度都是 1 。
那么关键点来了我们如何得到具有无限频率的信号呢,我们可以回想下无源振荡又或者开关部分的电路设计,是不是当开关下点的一瞬间可以理解为一个近似的冲激函数(幅度一般不会是无穷),而其又有无限个任意频率的信号,所以自然我们就想到把时域的冲激函数傅里叶变换到频域上会是什么情况
$$
F(\sigma(t)) = \frac{1}{2π}\int_{-\infty}^{\infty}\sigma(t)e^{-iwt}dt=\frac{1}{2π}
$$
由于冲激函数的选择性(分类讨论下即可)所以我们整理下可以得到
$$
1=2π·\sigma(w)
$$
做到这步也就完成了1的傅里叶变换。不过为什么这时候是把它展在频域上呢,我们可以由得到
$$
w=\frac{2π}{T}=2π·f
$$
这样是不是就很好理解1的傅里叶变换的过程,而且我们也理解了为什么说开关闭合一瞬间会有丰富的频率产生,所以如果你要一个固定频率的信号,其实可以利用开关+(理想)点通滤波器+电源
达林顿管
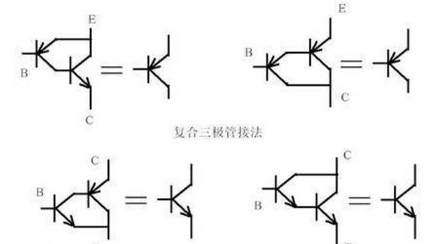
其实达林顿管就是复合三极管的结构,极性只认前面的三极管极性,主要作用就是实现高β,常用于实现功率放大器、稳压电源中
MOS管立体结构
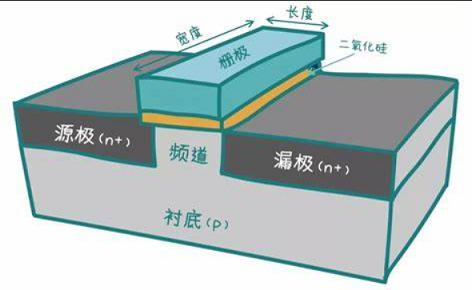
在很多时候,我们都关注于纸质书本上的平面图的理解,其实实际应用当中更需要有三维设计的能力。这也归功于上次我在看MOS管原理的时候突然想到对三维图像的不清晰
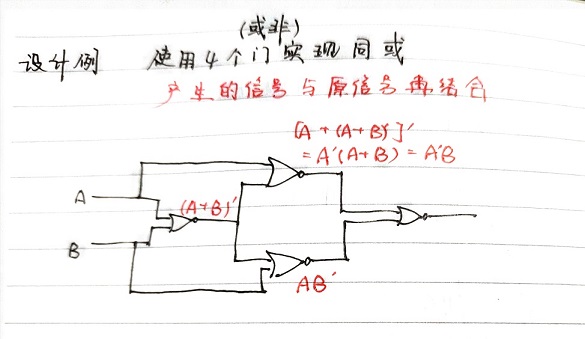
仅用四个或非门实现同或门
这周遇到的一个思考题,那就开门见山了,在电路设计的时候我们不一定所有信号都从原始的A、B等输入信号得来,需要同时考虑已有的中间信号再结合原信号,这样就可以节省一定的逻辑门个数。