发散性思维-点点思考-k与ε、单摆与LC谐振
主要讲讲为什么大物在学到库伦定律的时候不是再用高中所学的k而是利用1/4πε代替?单摆与LC并联谐振的公式推导怎么有点相似?
K与ε
$$
K=1/(4πε_0)
$$
经常用到的高斯定理
$$
\iint Eds=4πk \sum q=\sum q/ε_0
$$
此定理表述为:通过一个任意的闭合曲面S的电通量等于该面所包围的所有电量的代数和除以ε0
从这边其实很明显可以看出来,用真空介电常数替换后的式子会更加简洁,通过这边描述,可以知道其实ε0的引入是为了化简最后的某量表达式我们也可以看看麦克斯韦方程组得出的真空速度
$$
C=1/\sqrt(u_0ε_0)
$$
如果把ε0替换成K可想其表达式会有多繁琐
利用真空介电常数,可以在解决电介质问题(麦克斯韦方程组、电磁波波速表达式)时,使得答案变得比较简洁。
单摆周期公式
单摆的周期公式求解方法有很多,这边为了看出其与LC谐振的联系就选择从简谐运动的周期公式求解出发,这两者有一定的联系也是电训老师在上课偶然提起的
$$
F=ma=-kx
$$
由于简谐运动的位移为
$$
x=Asin(wt+\varphi)
$$
对此式进行求导,可以得到
$$
a=-w^2x
$$
故
$$
w=\sqrt(k/m)
$$
则运动周期为
$$
T=2π/w=2π\sqrt(m/k)
$$
在单摆的场景下回复力为
$$
F=-mgx/l
$$
即仅需把此时的k替换进行就可以得到单摆的周期
这边最主要的就是关于a的两个式子的联立带入
LC谐振
下面讲讲LC谐振的公式推导,模电嘛,它振荡了,唉它又稳定了嘿嘿,太经典了😂
这两天为了找到两者的关系废了好大劲,也算是对于谐振的原理有了一定的了解
LC谐振概念
LC电路可以称为储能电路、调谐电路,一般有两个作用
- 产生特定频率的信号
- 从多个特定频率复合信号中接收信号(这个就应用在后面我会讲到超外差式收音机)
其实如果从能量角度出发可以简单解释谐振的特点,我们可以这样想,如果一个电路输入信号一定,如果回路阻抗越小,是不是电路的能量就越大。
所以其实无论是串联谐振还是并联的谐振,都是令回路阻抗最小而导出此时输入信号的频率比如并联谐振(这个在前面电赛中的混沌电路就作为前级的信号发生电路)
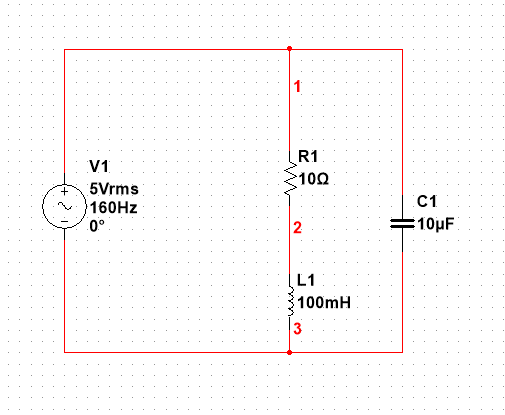
$$
Z=LC/(R+j(wL-1/wC))
$$
当下面式子满足时
$$
wL=1/wC
$$
回路的等效阻抗最小,电路谐振这边我们可以再回看下简谐运动所求的w,很明显两者是相近的,最后其实也是对简谐运动中的k进行替换就可以求出信号频率,这边就可以看出其相关方程形式是相近的,所以最后得到的答案当然是相似的
这边的话,对于谐振电路的谐振点我有个浅显的理解
- 对于并联谐振电路,我们可以把电容和电感产生的阻抗当作一个阻力,而信号是可以分开通过电容电感的,且总是通过阻力小的那边占多数,所以当两者阻抗不同时,总是有一边通过得多,这边相对于最佳的两者皆通肯定会有一个延时,只有当两者的阻抗相同时使得电路具有最大的能量。