发散性思维-点点思考-超外差式收音机混频、数字电路中输出端反相器的作用
最近电子实训课程发了个收音机让我们自焊,不只是要接收到电台声,当然也需要对其中的原理琢磨琢磨,这边就讲讲为什么混频后一定会出现输入信号频率和本振频率相差的频率?然后这周在进行数据选择器实验中,对于输出端的非门作用产生的疑惑,这边也讲讲其输出outbar的用意
本来是昨天打算写的,但是git_bash死了,今天终于给它救活了。
超外差式收音机原理
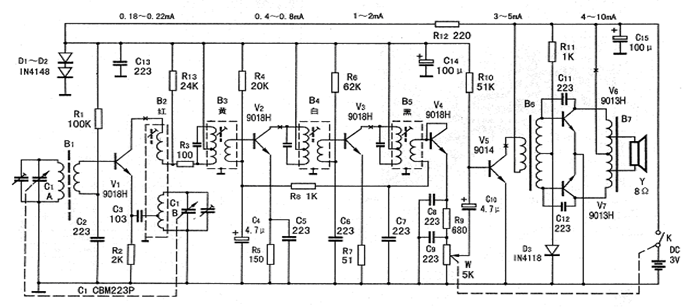
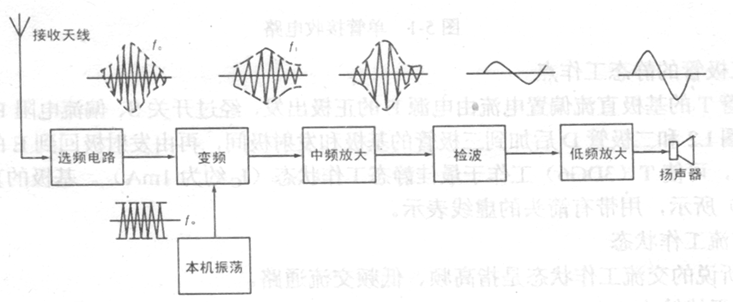
先讲讲七管收音机是如何工作的,把接收到的高频调幅信号的载波频率
$$
fc
$$
先变为频率较低而且是固定不变的中间频率
$$
f=465KHz
$$
再利用中频放大器加以放大。
方框图中的变频环节的作用是:把经过选频的高频载波信号的调幅信号和由本机振荡器产生的等幅高频信号,同时加到变频器上,由于变频管的非线性作用,就产生了
$$
f_i=f_0-f_c
$$
的差频信号,但仍为调幅波。因为差频低于载频而又高于音频,所以习惯上把它叫做中频(中周)。收音机的中频一般是465kHz。在选择电台过程中,本机振荡的频率随接收到的载波频率而变,并维持二者之差,使整个接收频段内均匀工作在465kHz左右,所以中频放大器的谐振回路就不需要调整,这样选择性也容易提高。这种形式的电路一般称为超外差式电路。中频信号经过放大后,仍然是频率比较高的调幅波,从中频调幅波中把音频信号检出来,也仍然称为检波。检波出来的音频信号再经低放(包括功放)电路去推动扬声器发音。
说到模拟电路模块的非线性特性这几年也是常常出现在各大电赛中,这边是利用了变频管的非线性特性,但是为什么就一定会产生本振信号和输入信号的差值信号呢?
下面就具体讲讲这个差值信号的来由
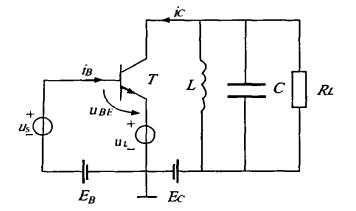
超外差式收音机中用到的三极管变频电路是射极注入方式,如图所示,本振信号从发射极注入。首先做出以下假设
$$
Us=Usm·cosw_st、U_L=U_mcosw_Lt
$$
相较于几十微伏或几个毫伏的天线电磁信号,本振信号有几百毫伏,则可以认为三极管变频电路是一个线性时变电路,也就是我们可以将三极管的工作点不受Us的影响。而集电极电流可以看成Ube的函数,所以
$$
i_c=f(E_B-u_L+u_s)
$$
此时对us用泰勒展开
$$
i_c=f(E_B-u_L)+f’(E_B-u_L)u_s+…
$$
通过量纲法我们可以知道上式中的系数项的单位为西门子,观察其中的宗量,可以知道其与输入信号和输出电流有关,且与时间有关,这边提出一个新概念
$$
g(t)=f’(E_B-u_L)
$$
g(t)就可以被称为时变跨导,下面把它进行傅里叶展开
$$
g(t)=g_0+g_1cosw_Lt+g_2cos2w_Lt+…
$$
则带入前面的ic的泰勒展开式其中的第二项为
$$
f’(E_B-u_L)u_s=g_0u_s+g_1cosw_Lt·u_s+g_2cos2w_Lt·u_s+…
$$
所以再利用下和化积公式就可以推出我们要的差值频率
$$
g_1cosw_Lt·u_s=g_1cosw_Lt·U_sm·cosw_st
$$
$$
ANS=1/2·g_1U_sm[cos(w_L+w_s)t-cos(w_L-w_s)t]
$$
而通过ic展开式us幂的丰富度可以知道肯定会有非常丰富的信号输出,但是其本身幅度就比较小,而且经过带通滤波的过滤作用就不予考虑在输出信号当中。
数字电路中输出端反相器的作用
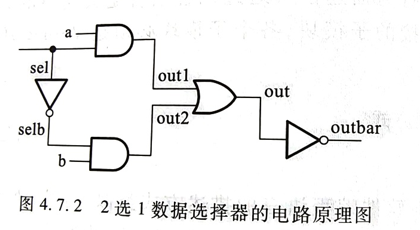
数据选择器是数电中常用的模块,这周也是在Robei上对其进行实验,然后就发现其输出端在原out的基础上又加了个非门,不禁引发了我的思考,下面是我的一些理解因为数据选择器知只是集成电路中的一个小模块,在使用过程当中必然要考虑其对于后级的影响,就像模电中要考虑负载的因素。这边最后再接入的反相器就是起到一个缓冲的作用。
而且在规模逻辑电路中常常利用非逻辑来进行设计会比较简易,即使用器件较少。