发散性思维-点点思考 (一)
今天是新学期网课的第一天,收获也是满满的感觉,涉及多个方面的点点思考
有趣一下:如何霸气地翻译
热评 我不是密接,我是阳性
首先聊聊今天数电课思考的零零散散
1. 思考格雷码的优点
我们先把3、4的格雷码和二进制代码的表示式写出来
| 编码顺序 | 二进制代码 | 格雷码 |
|---|---|---|
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
在二进制代码中 3切换为4 时,如果最右边的一位的变化比其他两位慢,就可能会在一个极短的时间中出现0101这样的状态,这个状态在系统运作中体现为噪声,而格雷码因为只有一位1的变化,所以并不会出现二进制代码出现的这种状况。
其实各种码制的出现就是为了让电路能正常工作在各种状态下。
2. 德 · 摩根定律理的一些理解与venn图推导
$$
(A·B)’=A’+B’
$$
$$
(A+B)’=A’·B’
$$
文字重演理解
反号分配入括号内的每个变量且内部的符号改变
图论 - - - Venn图
以第一个式子为例,其实第二个式子就是其对偶式。
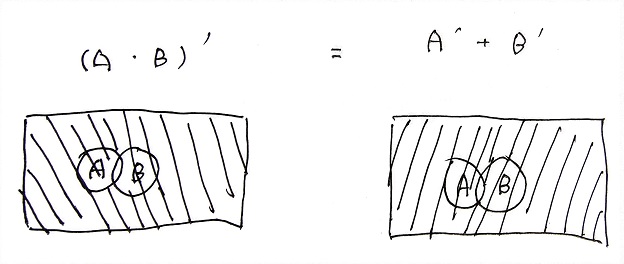
其实两种理解方法我觉得都挺好的,这也间接说明着,我们大学学科中渗透着高中的知识。
3. 与非门 相较于单用 与 / 非 门的优点
在数字逻辑电路设计中,用与非门比直接用与门和或门要节省器材,亦即节约成本。生产一个东西嘛,总是要考虑成本的一个与非门的功能至少要用一个与门或若干个或门及反相器才能实现。对相对复杂的电路而言问题则更加突出。元件数量 越多,电路的延时就越长,整个电路的频响性能就会变差,对高频电路而言则更加不划算。
跟模电中我们设计电路从分立的三极管电路到后面我们渐渐开始学运放的使用,关于运放的一点点点点的使用方法前面也有阐述,想要了解的可以康康。
4. 对偶定理与反演定理的关联和区别
不仔细地看,你会发现怎么两者好像是相同的但是实际上是不一样的。反演定理需要多做一步变量反置的操作。那对偶定理中的0 ---> 1、1 ---> 0是作用在哪?
然后经过我的surf发现,你康康下面的做法就可以顿悟
例如,若
$$
Y=A(B+C)+0
$$
这边我们给它加上一个零,其实相当于没有加,因为可以理解为加入了一个不可能事件。
然后我们在做对偶定理的操作后
$$
Y^D=(A+BC)·1
$$
这边就可以清楚地看到0、1变换是如何进行的,不过平常的话,因为这个操作并不影响实际的逻辑运算
结果,所以我们就没有体现出来。
对于反演定理一般就是用来逻辑运算,数字电路中如果要实现反相的效果,接个反相器就是了。
讲讲一个模电的东东
体二极管并不是有意做的二极管,是因为衬底和源极接到一起形成的。平常有的地方叫它寄生二极管,
这其实不太准确,因为如果不把衬底和源极接到一起就木有这个二极管的存在。
还有就是今天看到了群友发的冲牙器的设计技巧 - 硅胶塞

喷水时如果杯子密封够好,随着水量减少就会形成负压甚至真空,此时电机负荷就大了。加个硅胶塞中间有个孔,平常水漏不出去,一抽水形成负压后,外面空气从孔进去。
负压
相对于外界的大气压强,因为内部的水被电机抽走,水的体积流失的那部分需要原来容器内的空气来填补,所以内部的压强不断减小,使得容器内处于负压的状态。