信号抽取 - 奈奎斯特定理、带通采样

日常开发中采集信号常常说的至少利用2fH的采样频率来采集一个信号也就是奈奎斯特定理（低通采样定理），不过在RF射频领域中发射的电磁波常常在GHz往上。这时候如果再使用奈奎斯特定理直接采样，将使得需要极致的ADC性能，成本也相对不好接受

所以我们需要利用RF射频信号窄带的特性，使用带通采样定理进行信号采集

具体的推导过程就是保证频谱搬移之后的信号不产生混叠现象，以此得到fs和k的范围，满足此范围的fs都可以进行非混叠采样

下面具体讲讲FPGA实现带通采样的流程

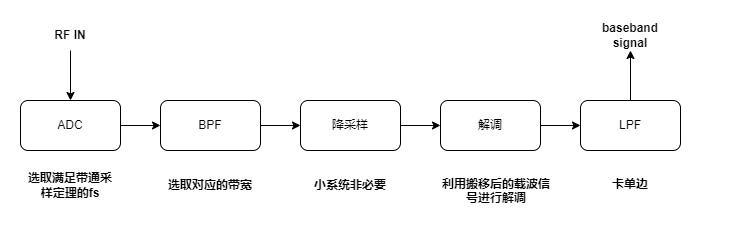
• 选取合适的ADC，并设置满足带通采样定理（上面的pdf中有相关推导）的采样频率fc
• 数字滤波器：设计fir or IIr滤波器，应该是BPF将采样后的信号进行滤波，去除频带外干扰，得到带通信号
• （小系统非必须）降采样：将滤波后的带通信号降低采样率（按一定时间间隔，抽取一部分信号样本），使其变成离散化的信号。主要目的：降低系统计算复杂度和存储开销
• 解调：将采样得到的带通信号乘以载波信号（非原始调制的载波信号而是新带通信号中心频率的载波信号）
• 结合理解上面这一步解调，我们也可以知道实际上带通采样就是将原始的载波信号搬移到一个较低频率，然后我们解调时自然就是需要利用新的载波信号对其进行解调 - 不理解的话可以看看后面我举的例子
• 数字信号处理：根据应用的需要，对解调后的信号进行进一步的数字信号处理（解码、去噪……）

RF_IN fH = 40M、fL = 39M、B=1M

例如选取fs = 8M利用带通采样的原理将接收到的调制信号频谱搬移到第一奈奎斯特区域也就是[7M 8M]，过一个带通滤波器（上下限卡一下双边），再利用7.5M的新载波信号进行解调，最后再过一个低通滤波器就可以得到基带信号篇[0 500k]

• 补：这边需要注意采样频率需要大于2B 即其范围修进位为（2B 2fH）

因为如果采样频率小于2B，那么假设这时候是第n奈奎斯特区域，有可能是跨在两个原频率带宽的中间，从而无法对信号采集完全

带通采样定理的应用

虽然这时候实现了采样频率的有效降低，但实际使用中不能因此使用采样频率太过拉胯的ADC，结合下面的ADC内部电路，实际上其可以看作是一个低通滤波电路，低采样频率的ADC相应的内置电容大，所以如果你高频信号进去就被滤没了