What is Mathematical Modeling

很久没更了，上次已经是去年8月份了哈哈！这期主要分享下近来的收获，不会具体到知识，更多的是方法论。AI时代下，只要我们想知识都是可获取的，而方法论不易。

1. 什么是数学建模，为什么要进行数学建模？

• 数学建模是在做将原来“不可解”的问题通过建立模型，使得问题变得”可解“，即降维。这边的可解与不可解是用计算量来衡量。
• 数学建模的目的就是预测未来。

2. 问题类型

1. 通过建立方程可以得到解析解
2. 可建立方程无法得到解析解
3. 无法得到方程

• 在工程中很多问题是属于无法得到方程，即知道要解什么，但是需要构建方程。
• 这类问题也是有方法论的，见下文。

3. 方法论

对于无法得到方程的问题，可分为两步，同时一般创新就出现在这两步中：

1. 抽象

   • 将我们的要解的对象进行抽象。
   • 抓住目标的本质。
   • 抓大放小。
   • 这一步抽象得好坏直接影响模型的优劣。

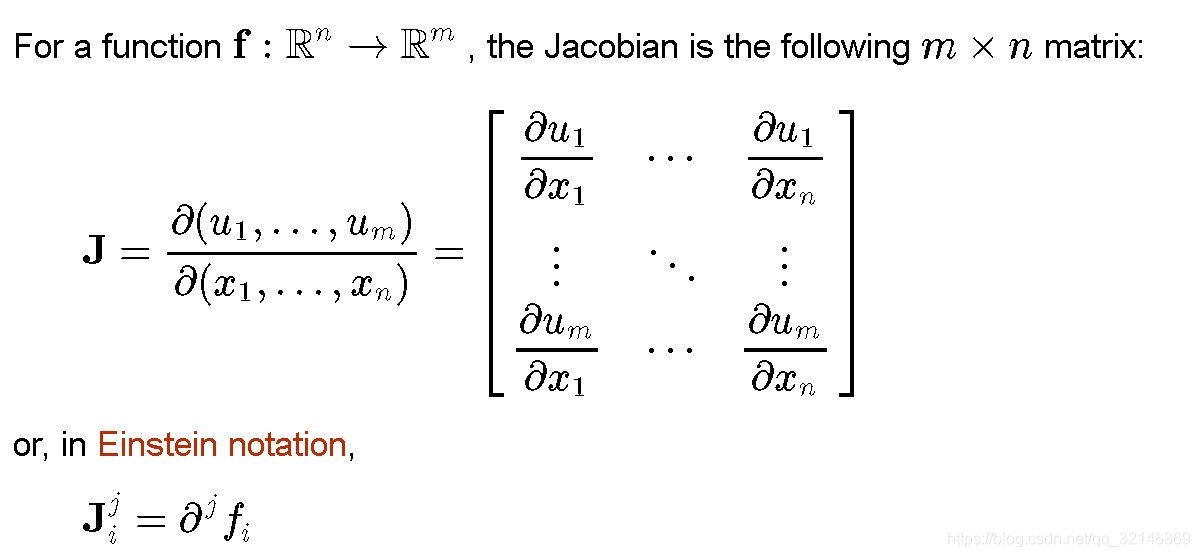
2. 创造方程（雅可比矩阵解决万物）

   假设方程形式为 f(x)=y

   • x是抽象出来的“解”，即我们要计算的。

     a. f(x)形式已知，直接通过雅可比矩阵可完成方程构造。这种情况可能构造出的方程不只包含x的一次式，比如可能包含x^2、e^x等。这可能是非线性方程组，一般采用数值解法或符号计算法。

     b. f(x)形式未知，数据分析或用AI猜？工程中常假设y与x呈线性关系，这样构造的雅可比矩阵的形式就是一个常数矩阵。

3. 这第二步的创新目前想到有两个，如果方程组很复杂怎么降维、近似？f(x)形式未知怎么构造方程？即怎么构造雅可比矩阵？

4. 上述属于抽象层交流，下面分享点其他

1. 矩阵相较于标量的优势太大了。
2. 矩阵真的很好！矩阵SVD分解、条件数、系数矩阵解稳定性、超定方程…
3. 难忘老师之前提到的和盛稻夫“努力到让神灵出手相助的地步”。关于雅可比矩阵这一通法是某一天晚上突然看到一篇文章突然联系起来的。