浅谈信号处理加窗修正

发表于 更新于 分类于 阅读次数： 本文字数： 2.9k 阅读时长 ≈ 3 分钟

• 引言

离散频谱校正在雷达测速和机械设备故障检测中起着非常重要的作用。由于信号的真实频率可能并不落在离散谱的整数根谱线上，所以如果不进行谱校正就达不到所要求的测频精度 。作为仪器仪表题大队的一员，信号处理是家常事。所以必然会接触到FFT测频，虽然在没加窗之前，测相对低频的时候精度已经不错，但是这没有发挥出FFT分析的优势。

所以这次就浅谈一下有点无敌的窗函数修正。最后精度差不多可以到0.0001%

• 理论分析

FFT测频原理

这边就需要先知道FFT分析完频率的计算公式
$$
f=K*fs/N
$$
其中K为ADC采样完的1024个数通过FFT运算得到的新数组（幅值数组）中最大的那一个数的下标位数、fs为采样频率、N为你使用的FFT分析数组个数

下面就是把ADC_Buff的处理幅值的Mag_Buff

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
for (uint16_t i = 0; i < FFT_LENGTH; i++)
	{
		fft_inputbuf[i] = (uint32_t)ADC_Buff[i] << 16;
	}

	// 计算
	cr4_fft_1024_stm32(fft_outputbuf, fft_inputbuf, FFT_LENGTH);

	// 计算幅值
	for (i = 0; i < FFT_LENGTH / 2; i++)	 //经过FFT后，每个频率点处的真实幅值  A0=lBufOutArray[0]/NPT
	{										 //                                 Ai=lBufOutArray[i]*2/NPT
		lX = (fft_outputbuf[i] << 16) >> 16; // lX  = lBufOutArray[i];
		lY = (fft_outputbuf[i] >> 16);

		X = FFT_LENGTH * ((float)lX) / 32768; //除以32768再乘65536是为了符合浮点数计算规律,不管他
		Y = FFT_LENGTH * ((float)lY) / 32768;
		Mag = sqrt(X * X + Y * Y) / FFT_LENGTH;
		if (i == 0)
			fft_outputbuf[i] = (unsigned long)(Mag * 32768); // 0Hz是直流分量，直流分量不需要乘以2
		else
			fft_outputbuf[i] = (unsigned long)(Mag * 65536);
	}

产生测频误差的原因

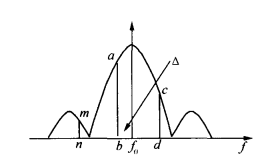
当分析点数为N时，信号采样频率为 fs ，频率分辨率就为 fs/N，这也被称为梳状效应。

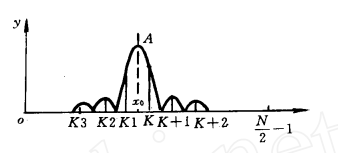
如果周期信号正好对正某一个整数根谱线，则得到的频率是准确的（不考虑计算精度误差）。这种情况也就是图中的 f0 谱线。而如果周期信号对正例如图中的b谱线时，那么就使得最终频率是不准确的。

加入窗函数的意义就是修正这个K值使得它对正于整数根（ f0 谱线）。

1. 矩形窗的应用

理论推导

虽然矩形窗被称为最一般的，但是我和辉在实际测过后发现矩形窗在FFT测频的精度时候会比汉明窗高。

最主要矩形窗实现的精度太高了，而且汉明窗越修正越离谱，我们就没有再尝试其他的窗函数。

设矩形窗
$$
w(t)=1 -T/2\leq\ t \leq\ T/2
$$

t在其他域内

$$
w(t)=0
$$

那么其傅里叶变换完是一个辛格函数
$$
w(f)=sin(\pi f T)/\pi f
$$
设输入时域信号x（t）为
$$
x(t)=P*e^{j(2\pi f_0t+\theta_0)}
$$
式中：P为信号幅度；f0为信号频率

其傅里叶变换为
$$
X(f)=P*e^{j\theta_0}\delta(f-f_0)
$$
从而可以得到该信号加矩形窗的频谱
$$
X_{rect}(f)=X(f)*w(f)
$$

设真实频谱在是f0处，而FFT的最高峰ab在谱线k处，幅值为L（k）；次高峰cd在谱线k+1处，幅值为L

（k+1）。其中谱线ab和真实频率f0的间距为△，那么次高峰与真实谱线的间距为1-△，显然|△|<=0.5。

由上面的加窗频谱得到

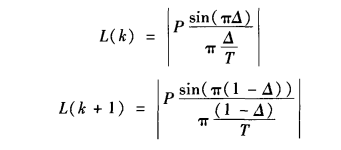
两式相比可以得到

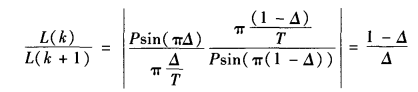
sin（π△）= sin π（1 - △）

然后就可以以此解出这个校正量△

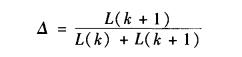
然后再分类讨论下就可以得到校正后的精确频率

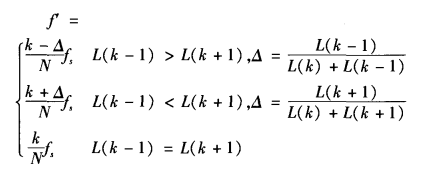
• 另法

其实修正的方法就是将通过最高峰和次高峰谱线求出中心的f0谱线，这边也可用重心法来求

实施代码

1
2
3
4
5
6
7
8
if (fft_outputbuf[index_fir + 1] >= fft_outputbuf[index_fir - 1])
{
	D = fft_outputbuf[index_fir + 1] * 1.0f / (fft_outputbuf[index_fir + 1] + fft_outputbuf[index_fir]);
}
else if (fft_outputbuf[index_fir + 1] < fft_outputbuf[index_fir - 1])
{
	D = fft_outputbuf[index_fir - 1] * -1.0f / (fft_outputbuf[index_fir - 1] + fft_outputbuf[index_fir]);
}

由于这边D修正系数数值是小于1的，所以为了防止被摆，导致最后修正的结果出乎意料。所以我们应

该预防这种情况，做个超幅置零的操作

1
2
3
4
5
if (D < -1 || D > 1)
{
	D = 0;
}
f = (index_fir + D) * Fs / FFT_LENGTH;

上述代码实现之后系统测出的频率精度应该就会让你眼前一亮。

2.汉宁窗

汉宁窗的理论推导这边就不详细说了，因为我们测频的时候效果一般。

如果想要了解的话可以康康下面两篇

基于窗函数的离散谱校正方法

频谱分析的校正方法

代码我也粘下：

1
2
3
4
5
6
7
8
if (fft_outputbuf[index_fir + 1] >= fft_outputbuf[index_fir - 1])
{
	D = (2 * fft_outputbuf[index_fir + 1] - fft_outputbuf[index_fir]) * 1.0f / (fft_outputbuf[index_fir + 1] + fft_outputbuf[index_fir]);
}
if (fft_outputbuf[index_fir + 1] < fft_outputbuf[index_fir - 1])
{
	D = (fft_outputbuf[index_fir] - 2 * fft_outputbuf[index_fir - 1]) * 1.0f / (fft_outputbuf[index_fir - 1] + fft_outputbuf[index_fir]);
}

虽然窗函数确实老厉害，但前提是你ADC、DMA等配置好了，有了基础的计算模型，窗函数才能锦上添花。而上述两个也是坑多，需要细心配置。提高测频精度的方法确实很多，这边也只是浅谈了其中一种。

比如你发现你的ADC采样频率对于信号频率来说过高，就算加窗，估计误差也不小，可以考虑下这个问题！